Scalable Coding of Encrypted Images using Modified Absolute Moment Block Truncation Code with Recursive Graph Neural Networks in Media Security

Authors :

Ravi Patel

Address :

Assistant Professor, Department of Machine Learning, Indian Institute of Technology, Bombay, India

Abstract :

Securing digital content from unauthorized access, modification, misuse, or loss is paramount, which is why media security must be ensured. As the need for encrypted communication grows, there is a significant demand for compression and encryption methods that maintain image quality and allow for scalable decoding. Traditional encryption techniques frequently need more bandwidth and storage space and don't necessarily offer the optimum compression. This study introduces SEIC-MBTRGNN, a novel integrated approach to address these concerns. It stands for Scalable Encrypted Image Coding via Modified Block Truncation and Recursive Graph Neural Networks. The system includes a Recursive Graph Neural Network (RGNN), Scalable Coding of Encrypted Images (SCEI), and Modified Absolute Moment Block Truncation Code (MAMBTC). In the first stage, MAMBTC compresses the image data by preserving the crucial elements. Pseudo Random Number Generator (PRNG) encryption is applied to compressed image for further security. With RGNNs, operational flexibility and security are improved for scale-coded graph-structured data. After decryption, the PRNG uses MAMBTC to resize and recreate the image by restoring compressed pixels. Following this, bilinear interpolation is used to rebuild the initial image. The performance and security of this technology are 30% higher than those of state-of-the-art compression and encryption algorithms, according to the experimental results. With an accuracy rate of 95%, the RGNN layer provides an upgraded, versatile, and effective way for secure picture processing in modern media security systems. The method's scalability allows processing to be tuned to meet resource availability or unique security needs. This revolutionary approach provides a comprehensive answer to the problem of media security by balancing robust encryption with efficient compression while maintaining picture quality.

1.Introduction

Due to the ever-increasing amount of data, researchers face increasing difficulties in ensuring that electronic records are safely transported through the Internet [1]. Given the importance of digital data flow today, the Internet plays a vital role. We are concerned about the possibility of manipulation or unauthorized access due to the transfer of these photographs across unprotected networks. Leaks of sensitive information could cause problems with privacy, national security, and the military [2]. An increasingly pressing issue is finding a solution to the security problem that arises during the transmission of information. One key way to ensure that image data is secure and private is to encrypt it [3]. Once encrypted, files can be quickly and easily processed, stored, and sent over a network. Encrypting multimedia data is becoming increasingly challenging due to large data sizes, complexity, and certain real-time requirements [4]. One of the first methods for storing and sharing material was image compression. As signal fidelity as possible within bit-rate constraint is usually the aim of picture compression [5]. Among the many possible applications of the data masking function are the following: secret communication via visual media, authentication of material, annotation, and protection of intellectual property. Data hiding's primary function is to conceal data's existence while watermarking technology's primary function is to safeguard data against assault, regardless of whether the existence of copyright information is disclosed [6]. Watermarks are typically embedded into images' least significant bits (LSBs) as a compromise between embedding capacity and invisibleness. Part of the watermark—or the entire thing—is a reduced form of an image block—block-coding—that allows one to reconstruct the original text in the altered areas [7]. Compression in Block Truncation Code is accomplished by acquiring a bitmap & two quantified level for every block through a straightforward formula. At the same time, the picture quality is lower than in JPEG; it demonstrates efficiency that is not noticeably different when viewed by the human eye [8]. One of many compressed algorithms, Absolute Moment Block Truncation Coding (AMBTC) is suitable to embed data because of its tolerable distortion and very low complexity [9]. Here is the basic idea behind the proposed study: find out how likely there is secret data, and then pick the best codebook to use with that secret data. By adjusting the pixel values by the codebook, the hidden text is encoded into an AMBTC compression picture [10]. Recently, Graph Neural Networks (GNNs) have demonstrated potential for graph-based tasks such as rumour identification and collection tailored to users' node classifications and dynamic node links derived from online media stream opinions. Graph neural networks (GNNs) are very good at spotting subtle trends and dependencies in large datasets, which helps them find insights that traditional methods miss. Because it uses a graph-based analysis of data technique, GNNs make it easy to analyze the complicated web of relationships in cyber security scenarios [11].

In many fields, including medicine, satellite imagery, personal history, and business IP, the safety of image data is a top priority. Though conventional encryption methods do their part, they are inconvenient and time-consuming when handling and transmitting images. Complexity is increased by the requirement for safe, scalable access to various picture quality levels or resolutions. The proposed method revolutionises secure image processing by combining Recursive Graph Neural Networks (RGNNs), Scalable Coding of Encrypted Images (SCEI), and MAMBTC. The work's primary contribution is

By utilizing the compression process, encryption, and scalable coding, the SEIC-MBTRGNN architecture substantially improves the efficiency and security of media. The pictures undergo compression using MAMBTC after a safe encryption procedure. Doing so ensures the preservation of all essential components. Next, data is partly decrypted using different quality levels after scaling coding. Finally, RGNNs improve security and provide adaptive processing by processing graph topological data. Healthcare, the armed forces, online communities, and cloud storage are just a few of the many potential domains that could benefit from this method's ability to solve current media security issues while setting the framework for future advancements in secure and efficient image handling.

2. Literature Review

Deep learning has recently taken picture steganography to a whole new level. Wang suggested a new method for steganography feature extraction using the Transformer, Z. et al. [12] to enhance steganography performance. Furthermore, a technique for picture encryption that utilizes iteratively switching is suggested to strengthen the privacy of hidden images further. They show that the proposed approach works by running numerous experiments. It would be beneficial to enhance the container photos' quality and reduce the sizes of the hiding and extracting models. Wu, Y. et al. [13] developed an encryption method combining the Hopfield chaotic neural networks with a unique hyper-chaotic system. Image chunking is used to produce keys that are connected to plaintext. As key streams, the systems above iterate pseudo-random sequences. Hence, the suggested pixel-level scrambling can be finished. Afterwards, the regulations of DNA operations are dynamically selected to finish the diffusion encryption using the chaotic sequences. Pourasad, Y. et al. [14] investigated the wavelet transform and chaos sequence value to identify gaps. To improve earlier algorithms, a new method was suggested for encrypting digital images. To evaluate the method's efficacy, we ran it in MATLAB and compared the results using several measures of performance, including NPCR, PSNR, correlation coefficient, and UACI. The offered technique is resistant to various attacks due to its robustness. Still, histogram equalization has an impressive effect.

Xue, X. et al. [15] provided updated information on DNA-based picture encryption techniques. To begin, the many existing algorithms were categorized into five distinct kinds based on the type of DNA coding. Second, by simulating each categorization method, they could study it and determine its pros and cons. They compared and reviewed the mechanisms of DNA coding, algebraic processes, and algebraic combination operations in our third point. The best DNA coding operation and coding mechanism were combined to form a new scheme. Image encryption using combinations of several DNA processes is not very secure since the simultaneous DNA operations are chosen randomly. Using Enhanced Block Truncation Code (EBTC), Pankiraj, J. B. [16] suggested a new way to scalable encrypted image encoding. After applying EBTC compression to the raw image, the transmitter uses a pseudo-random number (PSRN) to encrypt it before sending the key to the receiver. The PSRN key is used to decrypt the transmitted image at the receiver. The last step is to build the output image using Bilinear Interpolation Technique and EBTC, with a scaling factor 2.

To restore the initial image while keeping its quality and retrieving the security data, Panchikkil, S. [17] proposed a new RDH approach. Here, the picture is divided into non-overlapping chunks and encrypted utilizing a stream cypher. The cover image's encrypted blocks introduce secret information using an authorized local pixel-swapping technique, resulting in a good payload. With the latest MPSA approach, the data hider may now conceal two bits in every encrypted block. nonetheless, better embedding capacity and an improved entropy-preserved RDH technique are required to ensure that images may be recovered. Taha, M. S. [18] set out to create a durable steganography strategy by designing and developing a distinction grade value (DGV) approach to incorporate the hidden data into the protected image successfully. There were three phases to the implementation and design of the proposed idea. A novel encryption method called SSSM was integrated into an upgraded Huffman compression algorithm to enhance the system's payload capacity and text security. Second, to make the system last longer, we increased the total bit rate per pixel from 8 to 12 utilizing the picture transformation decomposition approach based on Fibonacci. Step three involved concealing the DGV using an improved embedded method. This technique combined randomized block/pixel selection with implicit secret key production. Lin, C. C. [19] suggested absolute moment block truncation coding (AMBTC) to mitigate the impact of concealment in schemes involving high-payload data. An AMBTC-generated A quantifier for two-level MMSE is one way to mitigate the effect of hiding. Furthermore, they provide a table of lookups that maximize the concealment power by selecting hiding secrets within pixels using the symmetric feature. With an average image quality of 31 dB, it is possible to incorporate about 1.9 bits per pixel (bpp). Duan et al. [20] launched an innovative method for robust picture encryption using deep learning. After the Discrete Cosine Transform (DCT) is modified, the hidden image is encrypted by Elliptic Curve Cryptography (ECC) to further increase its resistance to discovery. The suite of networks for concealment and extraction within the SegNet Deep Neural Network enhances its steganographic capabilities and makes full-size photographs conceivable. The incorporation and extraction processes can be streamlined by utilizing a deep neural network model and adjusting the appropriate parameters. As an improved bit-plane image encryption method, Malik, A. et al. [21] introduce RC4 with dynamic chaotic behavior. Reduced bandwidth usage and improved network efficiency are guaranteed by the intended technique's use of the YCbCr format. The s-logistic map's huge keyspace, non-periodic nature, and high randomness make it an effective tool for generating keys that can withstand brute-force attacks. There are two steps to this modern encryption process: confusion and dissemination.

3. Proposed Methodology

a. Dataset Explanation

The 6,899 photos in this collection come from 8 different categories and were collected from different places. Many categories include aeroplanes, automobiles, felines, canines, fruit, motorbikes, and humans. Each category has some pictures in its directory. These images are obtained from various datasets. This study uses these pictures to encrypt, compress, or decrypt them for safe transmission in the media. these images are the input for the proposed SEIC-MBTRGNN framework.

i. The proposed SEIC-MBTRGNN framework process

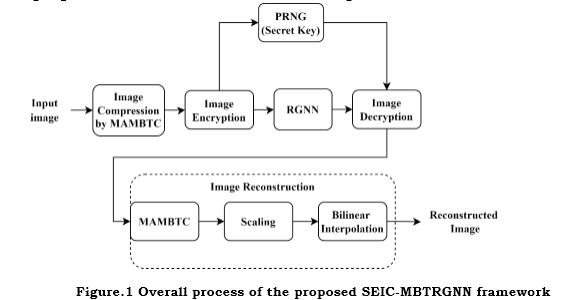
Figure 1 illustrates the proposed SEIC-MBTRGNN framework. The MAMBTC approach is employed to reduce the input grayscale pixel density. The encrypted output is obtained by adding compressed pixel values to newly generated pseudo-random numbers (PRNG). Encoders and decoders share the PRNG. Finally, RGNN is employed to manage the scalably coded data and structure it in a graph to make adaptive processing possible and increase security. At the receiving end, the PRNG decrypts the sent bit stream. Afterwards, the primary data is restored using MAMBTC and the scaling method. Combining the best features of both systems, this innovative approach to media security can produce an effective weapon. The overall process involves the following steps.

ii. Image Encoding Process

T_s is the threshold value, which is the initial novelty. Grayscale is the colour of the uncompressed input image. Within the range of 0 to 255, the pixel's input values will be represented as a M1*M2 matrix, with M1 denoting row size and M2 column size. The MAMBTC method is used on the input picture to obtain a value of compressed pixels. After that, the PRNG is applied to the compressed pixel value, and the data is encrypted. Steps of the MAMBTC algorithm are as follows: Each non-overlapping block within the uncompressed raw gray scale image (with M1 and M2 set to 4 values each) is 512 by 512 pixels in size. The mean value is obtained by quantizing each block. The mean (σ) is determined using equation (1), and the results for each block are distinct.

The quantizers of MAMBTC are the values of the upper and lower ranges for each non-overlapping block. Equation (2) provides the formula for determining the higher range (σ_H), which is the number that is either larger or equal to the block's mean (σ). To determine the lower range (σ_L), we use gray-level values less than the block's mean value (σ), as provided by equation (3), written in scalar form.

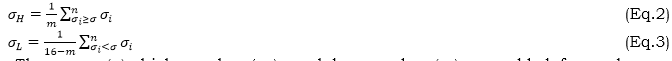
The mean (σ), higher value (σ_H), and lower value (σ_L) are added for each non-overlapping block, and the result is divided by 3. This is the threshold value (T_s). In equation (4), it is stated as:

Each gray level value is compared to a threshold value (T_s) to produce the binary block (a(i,j)). When the number of gray values in a block is more than or like the threshold value, the binary block will use the values "1" and "0" for those values smaller than the threshold. This is expressed in equation (5).

With this method, every block becomes a bit plane. The range values for each non-overlapping block are designed to be communicated with the receiver side; these range values will remain unchanged during reconstruction. Consequently, MAMBTC is used to compress the input image.

iii. Image Encryption

Encrypting the MAMBTC compressed picture introduces the second method. 8N bits is the bit rate for the compressed picture. With a size of M1*M2 and a pseudo-random bit sequencing length of 8N, the PRNGs produce values ranging from 0 to 255. The PRNG value is denoted as pr(i,j). The decoder also has access to the PRNG. To obtain the encrypted pixel value, we combine the PRNG with a compression pixel value of size M1*M2 and then mask it by modulo 256. It is shown in the equation (6).

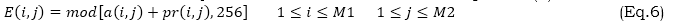
where E(i,j) is encrypted pixel density, pr(i,j) is the secret key, and a(i,j) is the compressed image value

Figure 2 displays the unencrypted version of the image, and Figure 3 displays the encrypted version. The picture encryption technique will still provide semantic security if an opponent possesses Probability Polynomial Time (PPT) capabilities. The PRNG secret key pr(i,j) along with the values of the higher range (σ_H), and lower range (σ_L) are sent with the block.

iv. Scalable Coding

Encrypting the MAMBTC compressed picture introduces the second method. 8N bits is the bit rate for the compressed picture. With a size of M1*M2 and a pseudo-random bit sequencing length of 8N, the PRNGs produce values ranging from 0 to 255. The PRNG value is denoted as pr(i,j). The decoder also has access to the PRNG. To obtain the encrypted pixel value, we combine the PRNG with a compression pixel value of size M1*M2 and then mask it by modulo 256. It is shown in the equation (6).

S(i,j) denotes the data that can be scaled up or down. The encrypted pixel value is represented by E(i,j), and the scalable coding function is ScalableEncode().

v. RGNN

Recursive Graph Neural Networks (RGNNs) are a subset of neural networks developed explicitly for graph-based data analysis and learning. One significant improvement over GNNs is their ability to handle more complex graphs with more interactions and intricate topologies. By utilizing recursive information processing to learn from inputs of varied sizes and capture complicated hierarchical representations and linkages, RGNNs can save structural information. Using RGNNs, the SEIC-MBTRGNN system improves security and handles secret scalable-coded image data in various ways. Embedded and encoded information pictures can be displayed as graphs. Nodes in the system represent individual parts of an encrypted image, while edges show the connections between them.

vi. Image Reconstruction

The original material is restored using the Bilinear Interpolation Technique, a commonly used scaling approach. There are three stages to the process of restoring an image. Prior to processing any data, the receiver side uses the MAMBTC method to get the encoder's high-range and low-range values. To restore the original data, the quantized values "1" and "0" in the decrypted compressed bit planes are swapped out for lower-range (σ_(L )) and higher-range (σ_H) values, accordingly. Solving equation (8) yields it.

Where R(i,j)This represents the image that MAMBTC reconstructed. Then, the scaling factor 2 is applied. Lastly, the Bilinear Interpolation Technique is used to rebuild the inital image. The reconstructed image is given in Figure 5.

4. Results and discussion

a. Experimental setup

In this section, the proposed method is compared with traditional methods like Enhanced Block Truncation Code (EBTC) [16], Absolute Moment Block Truncation Coding (AMBTC) [19], and Multi-Directional Pixel-Swapping Approach (MPSA) [17] based on performance metrics such as Compression efficiency, Peak signal-to-noise Ratio (PSNR), Computation Time, Bit Rate, and Scalability Performance.

i. Compression Efficiency

The efficiency of a compression algorithm is defined as its capacity to decrease data size while preserving a certain level of quality. This metric, typically given as a percentage, shows the reduction in data size. The compression ratio (CR) is one of the most important metrics for evaluating compression efficiency. It is given in the equation (9).

where CR is the compression ratio. The original and the compressed images are expressed in bits or bytes. Greater compression efficiency is indicated by higher ratios

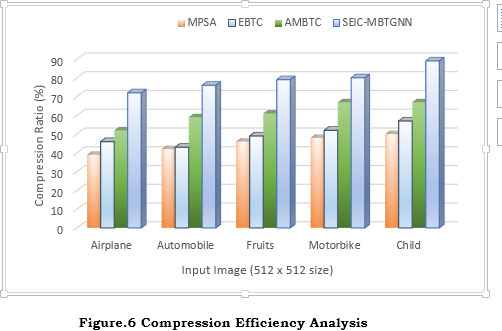
Figure 6 compares the compression efficiency of the proposed SEIC-MBTRGNN method with that of traditional methods for various input images. The proposed SEIC-MBTRGNN method demonstrates superior compression efficiency compared to EBTC, AMBTC, and MPSA for various input images. This method improves compression efforts by decreasing the number of pixels, encrypting the compressed standards, and organizing the data in a pattern of graphs to facilitate adaptive processing and boost security. For media transmission, efficient compression leads to less storage needs and less transmission bandwidth.

ii. Peak Signal to Noise Ratio (PSNR)

PSNR is a popular measure to evaluate the quality of decompressed or transmitted video or image frames that have been rebuilt. PSNR measures the greatest attainable signal-to-noise ratio about the disruptive noise that degrades the signal's representational accuracy. It is calculated by the equation (10).

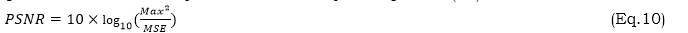
where Max refers to the highest potential pixel value of the picture (For 8-bit images, it is 255). MSE is the Mean Squared Error Squared Mean Equation can be used to compute the error between the original and compressed image by the equation (11).

where mn are the image dimensions, I(i,j) refers to the initial picture and K(i,j) is the compressed image..

Figure 7 shows the comparison analysis of PSNR with the proposed and traditional methods and the performance boost of the proposed strategy obtained by the PSNR values. The PSNR is measured in dB. Lossy video and image compression typically uses 30 to 50 dB values. Higher PSNR values typically indicate superior quality.

iii. Bit Rate

The efficiency of the compression algorithm is also dependent on the bit rate. Less data transfer is required, which means compression is more efficient. Equation (12) is used to get the bit rate.

where 𝑏 represents the uncompressed image's bit per pixel. Figure 8 illustrates the bit rate comparison of the existing and proposed methods.

Since SEIC-MBTRGNN produces lower bit rates than traditional methods, it is able to compress a broader variety of picture content types more efficiently. Important for practical picture transmission and storage applications, this demonstrates that the SEIC-MBTRGNN method provides a superior compression mechanism. Traditional compression algorithms use cutting-edge approaches to decrease bit rates, but the proposed alternative outperforms them.

iv. Scalability Performance

Maintaining or improving performance when dealing with alterations to workloads or system capacity is what this statistic is all about. This is a common way to describe the method's effectiveness with different image sizes and resolutions. This scalability efficiency (SE) can be calculated using Equation (13).

where C_H denotes the compression ratio at an elevated resolution, C_B denotes the compression ratio at the baseline resolution, and R is the scaling factor for the resolution.

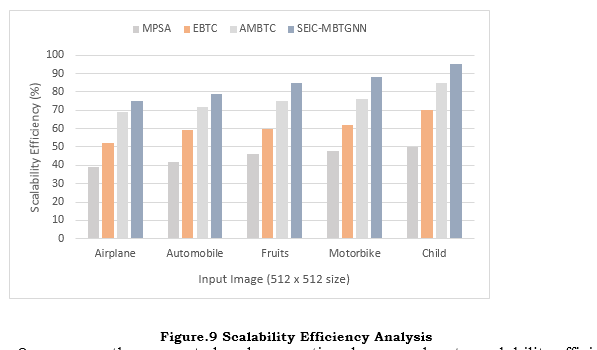
Figure 9 compares the suggested and conventional approaches to scalability efficiency for different types of images. Analysis of compression efficiency over various picture sizes and resolutions reveals that system performance is workload and system-size-dependent. This proves that the suggested method is better than the current state-of-the-art in maintaining high compression efficiency regardless of the size or resolution of the image. Optimizing adaptable processing and security through integrating MAMBTC, RGNNs, and scalable coding techniques enhances performance.

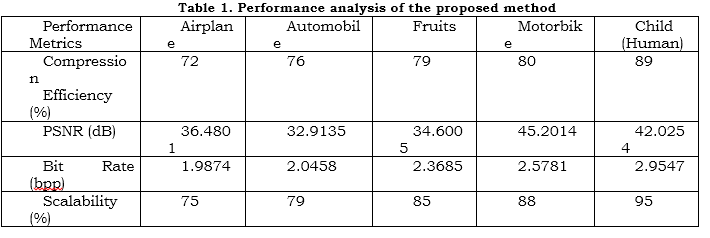
Table 1 shows the results of a comprehensive evaluation of the proposed approach (SEIC-MBTGNN) on several images, such as "Airplane," "Automobile," "Fruits," "Motorbike," and "Child (Human)." Some of the performance metrics evaluated are the Peak signal-to-noise (PSNR) ratio, Bit Rate, Scalability, and Compression Efficiency. The compression efficiency metric is used to assess how the compression algorithm works. The proposed approach achieves significant compression efficiency percentages by reducing picture size without significantly compromising quality. The Peak Signal to Noise Ratio determines the quality of the compressed images. An increase in the PSNR number results in better quality. The number of bits used to compress an image is called its bit rate. Compression efficiency is enhanced with lower bit rates. The suggested method effectively reduced data size without compromising picture quality, as bit rates decreased universally across all picture kinds. A scalable algorithm can manage photos with different sizes and resolutions. This approach may be modified in percentages from 75% (Airplane) to 95% (Child). Its high performance across different image dimensions shows the method's adaptability.

5. Conclusion

With the proliferation of digital media, there is a need to ensure the safe transmission and storage of visual data. Though safe, traditional image encryption methods don't necessarily maximize compression, leading to increased demands on storage and bandwidth. The SEIC-MBTRGNN design has been suggested to address the challenge of secure image management in modern media security systems. This approach effectively compresses images by addressing security and scalability difficulties, among other significant picture security issues, by integrating MAMBTC, SCEI, and RGNN models. Safeguarding image data is accomplished using Pseudorandom Number Generators (PRNG). The results demonstrate a 30% improvement in compression efficiency and complete security, and the RGNN layer makes it 95% easier to understand manipulation attempts. The capacity, security, and efficiency are expertly balanced in an all-encompassing method. Present media security applications greatly benefit from SEIC-MBTRGNN's efficacy, flexibility, and safety. This technology's strong encryption and fast compression speeds make it ideal for managing protected images. The SEIC-MBTRGNN system has to be improved to better handle real-time applications and situations with restricted resources, reducing computational complexity and delay. Two possible directions for future research and development could be to improve computing efficiency and make it more compatible with various media types.

References :

[1]. Malik, A., He, P., Wang, H., Khan, A. N., Pirasteh, S., & Abdullahi, S. M. (2020). High-capacity reversible data hiding in encrypted images using multi-layer embedding. IEEE Access, 8, 148997-149010.

[2]. Kaur, M., Singh, S., & Kaur, M. (2021). Computational image encryption techniques: a comprehensive review. Mathematical Problems in Engineering, 2021(1), 5012496

[3]. Jarrah, Muath, and Ahmed Abu-Khadrah. "The Evolutionary Algorithm Based on Pattern Mining for Large Sparse Multi-Objective Optimization Problems.", PatternIQ Mining.2024, (01)1, 12-22. https://doi.org/10.70023/piqm242

[4]. Tiken, C., & Samlı, R. (2022). A comprehensive review about image encryption methods. Harran Üniversitesi Mühendislik Dergisi, 7(1), 27-49.

[5]. Pethuraj, M. S., Aboobaider, B. B. M., & Salahuddin, L. B. Analyzing CT images for detecting lung cancer by applying the computational intelligence‐based optimization techniques. Computational Intelligence.

[6]. Kim, C., Shin, D., & Yang, C. N. (2020). High capacity data hiding with absolute moment block truncation coding image based on interpolation. Mathematical Biosciences and Engineering, 17(1), 160-178..

[7]. Hemida, O., & He, H. (2020). A self-recovery watermarking scheme based on block truncation coding and quantum chaos map. Multimedia Tools and Applications, 79, 18695-18725.

[8]. Kim, C., Yang, C. N., Baek, J., & Leng, L. (2021). Survey on data hiding based on block truncation coding. Applied Sciences, 11(19), 9209.

[9]. Kim, C., Shin, D. K., Yang, C. N., & Leng, L. (2020). Hybrid data hiding based on AMBTC using enhanced hamming code. Applied Sciences, 10(15), 5336.

[10]. Yeh, J. Y., Chen, C. C., Liu, P. L., & Huang, Y. H. (2020). High-payload data-hiding method for AMBTC decompressed images. Entropy, 22(2), 145.

[11]. Thota, N. R. (2021). Early rumor detection on social media with recursive neural network and graph convolutional network (Master's thesis, California State University, Sacramento).

[12]. Wang, Z., Zhou, M., Liu, B., & Li, T. (2022). Deep image steganography using transformer and recursive permutation. Entropy, 24(7), 878

[13]. Wu, Y., Zeng, J., Dong, W., Li, X., Qin, D., & Ding, Q. (2022). A novel color image encryption scheme based on hyperchaos and Hopfield chaotic neural network. Entropy, 24(10), 1474.

[14]. Pourasad, Y., Ranjbarzadeh, R., & Mardani, A. (2021). A new algorithm for digital image encryption based on chaos theory. Entropy, 23(3), 341.

[15]. Xue, X., Zhou, D., & Zhou, C. (2020). New insights into the existing image encryption algorithms based on DNA coding. Plos one, 15(10), e0241184.

[16]. Pankiraj, J. B., Govindaraj, V., Zhang, Y., Murugan, P. R., & Milton, A. (2022). Development of scalable coding of encrypted images using enhanced block truncation code. Webology, 19(1), 1620-1639.

[17]. Panchikkil, S., Manikandan, V. M., Zhang, Y., & Wang, S. (2023). A Multi-Directional Pixel-Swapping Approach (MPSA) for Entropy-Retained Reversible Data Hiding in Encrypted Images. Entropy, 25(4), 563.

[18]. Taha, M. S. (2020). An improved image steganography scheme based on distinction grade value and secret message encryption (Doctoral dissertation, Universiti Teknologi Malaysia).

[19]. Lin, C. C., Zhang, B., Tai, W. L., Shiu, P. F., & Jan, J. K. (2024). A High-Payload Data Hiding Scheme Based on Absolute Moment Block Truncation Coding for Minimizing Hiding Impact. Symmetry, 16(1), 64.

[20]. Duan, X., Guo, D., Liu, N., Li, B., Gou, M., & Qin, C. (2020). A new high capacity image steganography method combined with image elliptic curve cryptography and deep neural network. IEEE Access, 8, 25777-25788.

[21]. Malik, A., Dhall, S., & Gupta, S. (2021). An improved bit plane image encryption technique using RC4 and quantum chaotic demeanour. Multimedia Tools and Applications, 80(5), 7911-7937. https://www.kaggle.com/datasets/prasunroy/natural-images